Permutations and Frustrations

in which 8 years of endless attempts finally got the better of me.

Meet … the Bedlam Cube.

Orrrr at least that’s what it looked like when we bought it originally. For the last 8 years or so it has looked like this, or something similar.

At some point I decided enough was enough, time to write a solver.

A brief digression: a language I end up doing a lot of work in nowadays is Python, due to a specific plugin framework I’m responsible for. We’ve found it lacking in terms of performance frequently though, and often have to resort to C++ tools to handle the heavy lifting, with Python as an intermediary. My C++ could charitably be described as ‘rusty’, so my aim here was, uh, ‘thrice’fold:

• Write the solver in Python first then C++ to brush up on my C++
• Compare the performance of both implementations
• Find a solution for that goddamned bedlam cube so I could put the top on again for the first time in 8 years.

The Solution Space

The possible solution space is enormous. There are 13 pieces, so 13! (or 6,227,020,800) possible orders for the pieces to be added to the cube, for each piece there are up to 24 rotations (less for several of the pieces due to symmetries), and, generalising, 3x3x3 different positions they can be placed into the cube (which is 4x4x4).

There are 7 pieces with 24 unique rotations, 5 with 12 unique rotations, and 1 with only 3 (the cross piece). so (24^7 + 12^5 + 3) * 9 * 6227020800 = 257054422109169484800

257,054,422,109,169,484,800 different potential combinations. Hmmm. In reality of course given the nature of a recursive backtrack search method, many of these combinations will never be reached, entire search trees will be pruned after only 2 or 3 pieces are added and a non viable solution is detected. Still. It’s a big number.

Apparently there are 19,186 different solutions, so even considering only the order in which you add the pieces there’s only one solution for every 324,560 permutations. And I wondered why I never managed to solve the thing.

Visualisations

I knew I would have to build out the state and internal representation of the pieces and ongoing solution, so the first thing I did was put together a quick visualisation library to allow me to sanity check what I was doing.

I generalised out the representation of the problem so I could try simpler ones, a pretty straight forward JSON file describes the dimensions of the cube and the pieces . This is the one for the full Bedlam problem:

{
    "shapes":[
        {"colour":"#6495ed", "name":"Little Corner", "blocks":[[0,0,0],[0,0,1],[1,0,0],[1,1,0]]},
        {"colour":"#00ff00", "name":"Spikey Zag", "blocks":[[0,0,1],[0,1,0],[0,1,1],[1,1,0],[1,2,0]]},
        {"colour":"#ff00ff", "name":"Pokey Corner Bit", "blocks":[[0,0,0],[0,1,0],[1,1,0],[0,1,1],[0,2,0]]},
        {"colour":"#ff69b4", "name":"Right Angles Everywhere", "blocks":[[0,0,0],[0,0,1],[0,1,0],[0,2,0],[1,2,0]]},
        {"colour":"#4b0082", "name":"Middle Zig", "blocks":[[0,0,0],[0,1,0],[0,1,1],[1,1,0],[1,2,0]]},
        {"colour":"#2f4f4f", "name":"Pokey Z", "blocks":[[0,0,0],[0,0,1],[0,1,0],[1,1,0],[1,2,0]]},
        {"colour":"#8b4513", "name":"Corner Joist", "blocks":[[0,0,0],[1,0,0],[0,0,1],[0,1,0],[0,2,0]]},
        {"colour":"#f5deb3", "name":"Dented L", "blocks":[[0,0,0],[1,0,0],[1,0,1],[0,1,0],[0,2,0]]},
        {"colour":"#00ffff", "name":"F in Therapy", "blocks":[[0,0,0],[0,0,1],[0,1,0],[1,1,0],[0,2,0]]},        
        {"colour":"#0000ff", "name":"Flat M", "blocks":[[0,1,0],[1,0,0],[2,0,0],[1,1,0],[0,2,0]]},
        {"colour":"#228b22", "name":"Cross", "blocks":[[0,1,0],[1,0,0],[1,1,0],[2,1,0],[1,2,0]]},
        {"colour":"#ff0000", "name":"Confused F", "blocks":[[0,0,0],[1,0,0],[1,1,0],[2,1,0],[1,2,0]]},
        {"colour":"#ffff00", "name":"T-Bone", "blocks":[[0,1,0],[1,0,0],[0,1,1],[1,1,0],[1,2,0]]}
    ],
    "width":4,
    "height":4,
    "depth":4
}

Each of the shapes has a colour, a unique (and mostly nonsensical) name, and a series of [x,y,z] triplets representing each of the individual cubes that make up the shape.

I used the Python Imaging Library PIL (or rather the pillow fork) to put together a quick visualisation, PIL makes it easy to read and write PNGs and tile them onto a framebuffer etc. The first thing I did was write out all the piece configurations to sanity check the setup:

So far so good. The next thing I wanted to do was pre-process the rotations for all the pieces, and eliminate duplicates. My hacky viz library allowed me to sanity check that as well, i.e. for one of the pieces with 24 rotations:

For one of the more symmetrical shapes with 12 rotations:

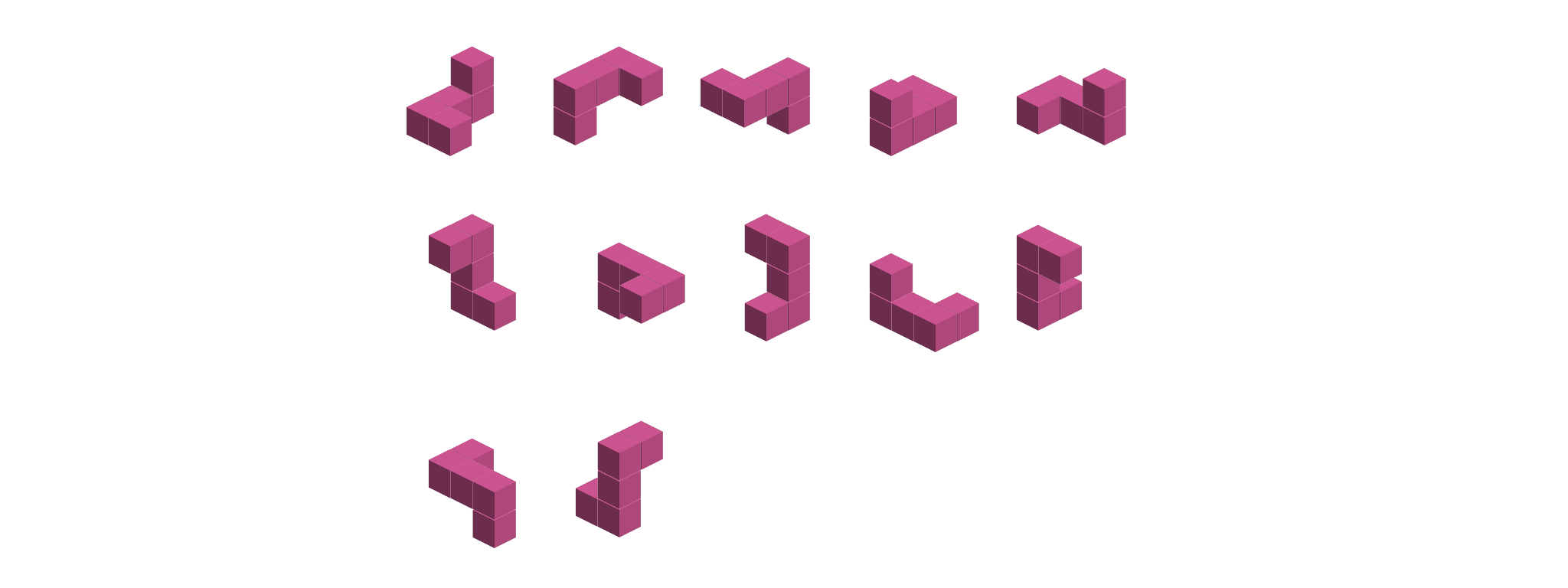
And for the one shape with only 3 rotations:

These were built up using this single base piece offset in the X and Y axes to produce an isometric view of the composite shapes, and coloured appropriately.

The Solver

After pre-computing the rotations for the shapes and eliminating duplicates, the Cube state is set up, stored in cube.py or cube.cpp depending on which solver is being used, then the permutation generator kicks off, and calls into the recursive shape placer.

In neat psuedo code, to find the first solution for a specific permutation, it basically looks like this:

for every permutation of shapes, starting with the first shape in the array:

RECURSIVE:

    if this is being called for a shape index that's > number of shapes in the 
    array, then congratulations, we have a solution, so return True to bail out 
    of the entire block.

    for x in 0 to Cube width:
        for y in 0 to Cube length:
            for z in 0 to Cube depth:
                for every rotation of this shape:
                    try to put this rotation of the shape into the cube at x,y,z 

                    if it CANNOT be placed, return false

                    if it CAN be placed, call this same RECURSIVE for the NEXT shape 

                    if the NEXT shape can't be placed, then REMOVE this shape from                         the cube again, and move onto the next rotation, then the next 
                    depth, then length, then width, then eventually bail out and try 
                    another permutation of shapes.

This is expressed rather more eloquently in code form here in Python and C++

The python code actually stores a running list of solutions as it goes, until it hits a specified ‘num_solutions’ and then bails, the C++ solver finds the first solution and then quits.

C++ / Python

I wrote the Python solver first, because I’m more comfortable footling around with Python than with C++. The C++ code I wrote duplicates the main recursive loop and the state handing of the Python, but relies on the Python code to do all the prep work, loading the JSON and calculating the different rotations. It also hands off the solution (if/when found) to the Python code to render the viz. No point writing any of the non-performance critical stuff twice.

The Solutions

It shouldn’t come as a surprise to discover that the C++ code, functionally identical to the Python code, outperformed its interpreted cousin by a country mile. I kicked this off on Sunday evening, and these were the eventual results.

C++

Sun Oct 31 22:36:57 GMT 2021
Mon Nov  1 00:18:14 GMT 2021
1 hour, 42 minutes and 0 seconds

For a total of 102 minutes, not too shabby.

Python

Sun Oct 31 22:36:37 GMT 2021
Wed Nov  3 08:52:02 GMT 2021
2 days, 10 hours, 16 minutes

This was a total of 3496 minutes

Yikes, so the Python solver was ~34 times slower than the equivalent C++ code.

Of course there was a suitably impressive viz of the solution. This got built up similarly to the shapes images above, with the addition of the background ‘Cube’ image, and with each of the shapes being added in turn to the cube. Each row displays… 1. the specific shape 2. the rotated shape in the correct position in the cube 3. the cumulative solution

Conclusion

Well, yes, Python is an order of magnitude slower than C++ for something like this. For the most part of course, it’s not iterative solutions or endless computation we’re waiting on, it’s things like disk IO, or some data retrieval over the network, or similar. Nonetheless, it’s a good example to pull out when someone suggests writing something a little busier in Python. C or C++ is probably the way to go. For everything else, Python is as good as any, and it’s easier to iterate quickly on this sort of messy json manipulation, permutations of arrays, etc in Python over C/C++.

I was forced to use CMake recently (for the Pico C++ SDK while writing this Keyboard firmware) and spent a lot of time cursing its black black heart. This was before I embarked on trying to get a simple Make build to work for the C++ bit of this solver. It was one of those epiphanies so common in the engineering world. “Ah, and I thought the PREVIOUS tool was bad”. Long story short, I gave up on Make and did up a very simple CMakeLists.txt and it worked just fine. Lesson learnt.

Shout out to Niels Lohmann’s rather amazing JSON Library for C++, without which this would have been a lot harder.

Full source is available on github here:
https://github.com/dairequinlan/bedlam-solver